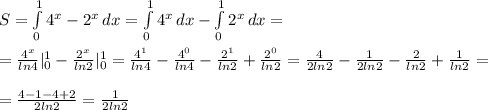Найти площадь фигуры, огранниченной линиями y=2^x, y=4^x, x=1
Другие вопросы по теме Алгебра
Популярные вопросы
- №290 подбери прилагательные противоположного по значению. лисица хитрая,...
1 - X^(log4(x)-2)=2^(3*(log4(x- ,сам решал ,не могу...
3 - Информация, хранящаяся в долговременной памяти компьютера как единое целое...
1 - Вларёк 28 корзин огурцов, по 30 кг в каждой. 15 корзин продали. сколько кг...
3 - Сначала запишите глагол, от которого образовано причастия,укажите вид глагола.затем...
1 - Подберите однокоренные слова к слову доверие...
3 - Книжный фонд библиотеки расположен в четырёх комнатах. в первой находится...
2 - Округлите до сотых: 3,062; 4,137; 6,455....
3 - Составить план ( 3 пункта плана) к рассказу пермяка е. случай с кошельком....
3 - Мальчик от дома по направлению на запад 1200 м. затем повернул на север и...
3
Как видно из рисунка который я приложила к решению нужно найти площадь заштрихованной фигуры. Площадь это интеграл, по х от 0 до 1 верхняя граница это 4^х нижняя - 2^x. То есть площадь выражается: