Найти первообразную функцию f(x), график которой проходит через точку m1) f(x) =2x^2-3x, m(2; -3)2) f(x) =x^3, m(-1; 10)3) f(x) =-x^2+x, m(2; 0)4)f(x)=-x^3, m(1; 3)
Другие вопросы по теме Алгебра
Популярные вопросы
- Вкакой форме хранится звук в компьютере...
3 - Дощ іде.хмари пливуть.вітер віе-синоніми....
2 - Britain s first astronaut, 27- year - old helen sharman from...
2 - Найдите значение выражения 2,1*10^2+3.8*10^3...
3 - Площадь, занимаемая китаем составляет 9 600 тыс. км квадратных,...
3 - Начерти прямоугольник, ширина какого ровно 25мм, а длина у 2...
3 - Алина в магазине купила 2 кг сахара по цене 29р за 1 кг и 0.5кг...
2 - Найдите значение ! 6 в степени 2log 6 (12)...
1 - Прочитайте предложения и определите наклонение выделенных глаголов....
1 - 1. одна из замечательных особенностей голубей – умение вернуться...
2
1)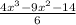
2)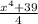
3)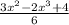
4)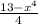
Объяснение:
Сначала нужно проинтегрировать функцию f(x), чтобы найти ее первообразную, затем выразить константу и подставить вместо x и y координаты точки M:
1)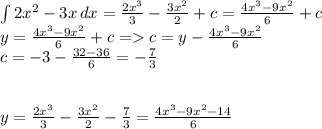
Первое я расписал подробно, чтобы было понятно, что происходит. Дальше будет более кратко.
2)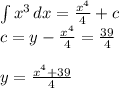
3)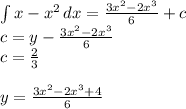
4)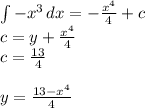
(Что-то встроенный редактор формул какой-то кривой, всё перемешалось)