Найти остаток от деления числа

8

Объяснение:

Найдём функцию Эйлера от числа 15. Это количество чисел, меньших 15 и взаимно простых с ним, то есть не имеющих с 15 общих делителей. Такими числами являются 1, 2, 4, 7, 8, 11, 13, 14, поскольку они не делятся ни на 3, ни на 5. Тогда функция Эйлера φ(15) = 8.

Так как 2 и 15 — взаимно простые числа, то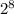 сравнимо с 1 по модулю 15.

Тогда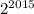 можно записать в виде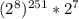

Поскольку мы выяснили, что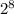 сравнимо с 1 по модулю 15, то 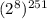также сравнимо с 1 по модулю 15.

Остаётся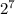 , которое сравнимо с 8 по модулю 15, поскольку даёт остаток 8 при делении на 15.

То есть можем записать: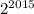 ≡ ≡ 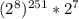≡ 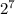8 mod 15

Это значит, что остаток равен 8.