Найти остаток от деления 7^60 на 143 используя малую теорему Ферма

ответ: 1

Объяснение:

Добрый вечер!

Заметим, что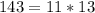

Малая теорема Ферма гласит, что для любого простого числа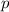 и натурального числа 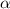, где 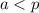  , справедливо равенство:

Найдем: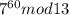  

Заметим, что число 13 простое, причем 7<13, тогда можно применить малую теорему Ферма:

Другими словами:

, где - натуральное число

Заметим, что в биноме Ньютона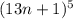 все члены, кроме члена 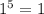, помножены на некоторую степень числа 13, а значит данное выражение дает при делении на 13 остаток 1.

Найдем: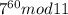

Число 11 простое, и 7<11, тогда рассуждая аналогично имеем:

Таким образом :

,поскольку 11 и 13- взаимнопростые