1. Алгебра
  2. найти ошибку 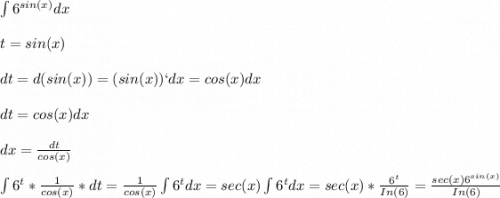При дифференцировании

найти ошибку \int\limits6^{sin(x)} dx t = sin(x)dt = d(sin(x) ) = (sin(x))`dx = cos(x)dxdt = cos(x)dxdx=\frac{dt}{cos(x)} int\limits6^t*\frac{1}{cos(x)}*dt = \frac{1}{cos(x)}\int\limits6^tdx = sec(x)\int\limits6^tdx = sec(x)*\frac{6^t}{In(6)} = \frac{sec(x)6^{sin(x)}}{In(6)}

При дифференцировании полученной первообразной я получил абсолютно другую функцию:


Вопрос: где я допустил ошибку во время интегрирования?


(\frac{sec(x)6^{sin(x)}}{In(6)})` = \frac{1}{In(6)}(sec(x)6^{sin(x)})` = \frac{1}{In(6)}[(sec(x))`6^{sin(x)} + (6^{sin(x)})`sec(x)] =\\= \frac{1}{In(6)}[tg(x)sec(x)6^{sin(x)} + In(6)cos(x)6^{sin(x)}sec(x)] = = \frac{1}{In(6)}[\frac{6^{sin(x)}sin(x) }{cos^2(x)} + In(6)6^{sin(x)}] = \frac{6^{sin(x)}sin(x) + In(6)6^{sin(x)}cos^2(x) }{In(6)cos^2(x)} = = \frac{6^{sin(x)}sin(x)}{In(6)cos^2(x)} + 6^{sin(x)}

ssha2 ssha2    2   08.06.2021 18:15    0

Ответы
Tima22890 Tima22890  08.07.2021 18:15

Объяснение:

У 6-му рядку   помилково винесено з-під знака інтеграла 1/cos(х).  А це зробити не можна ,  так як   х  залежить від  t і так само від  t залежить і  1/cos(х) .

ПОКАЗАТЬ ОТВЕТЫ
mebelru mebelru  08.07.2021 18:15

Нельзя выносить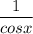   \dfrac{1}{cosx}   за знак интеграла, т.к. там содержится переменная "х" ... Надо было выразить "х" через "t" и найти dx :

\displaystyle t=sinx\ \ \Rightarrow \ \ \ x=arcsint\ \ ,\ \ dx=\dfrac{dt}{\sqrt{1-t^2}}\\\\\\\int 6^{sinx}\, dx=\Big[\ t=sinx\ \Big]=\int \frac{6^{t}\cdot dt}{\sqrt{1-t^2}}

\star \ \ \displaystyle \int 6^{sinx}\, cosx\, dx=\Big[\ t=sinx\ ,\ dt=cosx\, dx\ \Big]=\int 6^{t}\, dt=\frac{6^{t}}{ln6}+C=\\\\\\=\frac{6^{sinx}}{ln6}+C\ \ \star

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
kallor12 kallor12  25.04.2020 16:25
Найди наибольшее и наименьшее значения заданной функции на заданном отрезке без производной: y=−5x4+5, [0;5]....
Kartrider Kartrider  25.04.2020 16:25
Ка з наведених пар чисел є розв’язком рівняння -5х+2у=8? А.(-2;9) Б.(-4;-6) В.(3;6) Г.(-6;11)....
эаэаэа эаэаэа  25.04.2020 16:25
На фотографии, у меня вышло -1 но это неправильно я думаю​...
SuperMaksni4ic SuperMaksni4ic  25.04.2020 16:24
Найдите найбольшее значение выражения ​...
ГЛУПАЯДОМАШКА ГЛУПАЯДОМАШКА  25.04.2020 16:24
Запишіть квадратний тричлен у вигляді добутку: х2 - 5х + 6 , х2 - 4х - 5...
wannaone wannaone  18.02.2021 12:26
Задание N 2 состоит из одного условия Запиши недостаюшие компоненты в каждом из 5 примеровf) (+ + 2в)? = a* + 4ав + 4в?2) (3х + *)* = 9х2 + 6х +13) (++ 2т)= = 100...
Tania22012003 Tania22012003  18.02.2021 12:27
Тело массой т кг движется по зако ну x(t)(х - в метрах, t — в секун дах). Найдите силу, действующую на тело в момент времени tо, если ЕСТЬ ФОТО, УМОЛЯЮ...
Ппмммммммм Ппмммммммм  18.02.2021 12:27
№2. Объект запущен с платформы. Высота выражается формулой h=−¿, где h-высота в м, t-время в секундах.1)Найди высоту платформы2)Определи, через, сколько секунд предмет...
irapodumey irapodumey  18.02.2021 12:28
3. Реше задачу. В областной математической олимпиаде Пифагор привяли уча-стие 69 детей из городских школ и 93 - из сельских. Каждая шко-ла отправила по 3 ученика....
Mesia14 Mesia14  18.02.2021 12:28
Функцію задано формулою у = -2х – 4. Знайдіть: а) у(-1), y(1);б) значення аргументу, при якому (x) = -1, y(x) = 1;в) координати точок перетину графіка даної функції...

Популярные вопросы