Найти общий интеграл дифференцированного уравнения
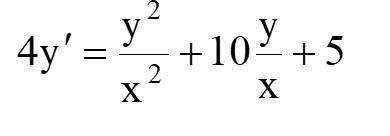
Другие вопросы по теме Алгебра
Популярные вопросы
- Исходные вещества для получения сложных эфиров: а. карбоновые кислоты и...
1 - Как решить от точки а до точки в расстояние равно 3 см. отметь еще 15 точек...
3 - Сколько корней имеет квадратный трехчлен -х в квадрате +6х-10...
3 - 1) свойство воды: разложение, отношение к натрию, кальция, оксиду серы...
3 - Сумма двух чисел ровна 67 30% от первого и 58% от второго в сумме состовляют...
2 - Симметрия в . в чем она выражается?...
3 - Твір-роздум на тему милосердя норма життя чи поодинокий випадок джеймс...
3 - В1м3 5 граммов водяного пара определите при какой температуре относительная...
1 - Вхлороводородную кислоту взятую в избытке опустили в смесь содержащюю цинк...
3 - Возможно ли счастье без добра ? что вы думаете по этому поводу? напишите...
1
однородное ДУ
Замена:
общее решение