Найти общее и частное решение
y''-8y'=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишате смысел пословицы голодный француз и вороне рад...
2 - Много найдите ошибки или неточности в тексте. исправьте их. нуклеотид...
3 - На сегодня мне нужно перечеслять про проблемов городов. например:...
2 - Прочитайте выражения,найдите их значения.разбейте полученные...
3 - Вот мне задали такое : занеси в тетрадь все изменения биоритма...
1 - Расстояние от меркурия до солнца равна 57,90 млн км как эта величина...
3 - Число электронов во внешнем электронном слое атома, ядро которого...
1 - Решить ! какую скорость разовьет тело массой 2 кг через 5 сек,...
1 - 87-41+у)=22 решите нормально уравнение...
1 - Напиши будь ласка,поширення речення ростуть квіти...
1
Составим и решим характеристическое уравнение:
Запишем общее решение:
Запишем частное решение. Пусть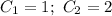 :
: