Алгебра: Найти область значений функций.

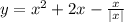
$y = x {}^{2} + 2x - \frac{x}{ |x| }$
Найти область значений функций.

Ответы

dedavydov12 09.01.2022 14:10

$y=x^2+2x-\frac{x}{|x|}$ , ОДЗ: $x\ne 0$ .

Определение модуля: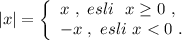 $|x|=\left\{\begin{array}{l}x\ ,\ esli\ \ x\geq 0\ ,\\-x\ ,\ esli\ x$

Поэтому заданную функцию можно записать в виде :

$y=\left\{\begin{array}{l}x^2+2x-1\ ,\ esli\ x0\ ,\\x^2+2x+1=(x+1)^2\ ,\ esli\ x$

Построим график функции . Точки , через которые проходит график: (-3:4) , (-2;1) , (-1,0) , (1;2) , (2;7) .

По графику определим, что область значений функции

$E(y)=(-1\ ;\ 1\ )\cup (\ 1\ ;+\infty )$ .

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

ayratka2 18.07.2019 04:10

Как звали главного героя из сказки малыш и карлсон...

Ильяна111 18.07.2019 04:10

мейрбек2 18.07.2019 04:10

Asil1231 09.12.2020 11:05

shoistakarimova 09.12.2020 11:06

dzeratigieva 07.09.2019 13:00

Найти корни квадратного трехчлена 5х² - х - 6...

pumferplay 07.09.2019 13:00

МиленаГригорьева25 07.09.2019 12:50

Dania0609 07.09.2019 12:50

Сократите дробь: 12-3x 16-x2(x - в квадрате)...

Toxichnui 07.09.2019 12:50