Найти область значений функции у=1/(sin^4(x)+cos^4(x))

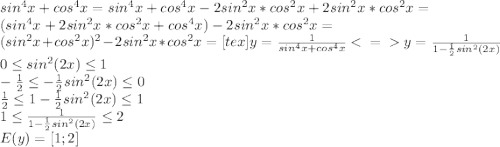" alt="y= \frac{1}{sin ^{4} x+cos ^{4} x} \ \textless \ =\ \textgreater \ y= \frac{1}{1- \frac{1}{2} sin ^{2} (2x)} \\ 0\leq sin ^{2} (2x) \leq 1 \\ - \frac{1}{2} \leq - \frac{1}{2} sin ^{2}(2x) \leq 0 \\ \frac{1}{2} \leq 1- \frac{1}{2} sin ^{2} (2x) \leq 1 \\1 \leq \frac{1}{1- \frac{1}{2} sin ^{2} (2x)} \leq 2 \\ E(y)=[1;2]" />" />