Найти область сходимости степенного ряда.
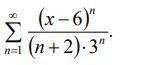
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите сочинение на тему: Что нового и интересного я узнал о Пушкине,...
1 - В прямоугольном треугольнике один из острых углов равен 60 градусов а...
2 - 28% of a number is 168. Find the number....
3 - Эл 349. а) Составьте предложения из слов каждой строч-ки. Поставьте имена...
2 - Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй...
2 - 1.1 ПОЛІКІelepді ЖHнақтай отырыптақырып бойынша постер жасау Ұзақтығы...
2 - Укажите одночлен стандартного вида 1) -7abac 2) -1,4ab·5ac 3) -7ba²c...
1 - 2. Задание. Найди периметр прямоугольника разными если а-длина Если б-ширина...
1 - 1.Объясните значение фразеологизма работать на совесть, который встретился...
2 - 5. За малюнком доведіть, що ДАВС = ДМСВАМІНHнСВ...
3
ряд условно сходится (по признаку Лейбница) .