Найти область сходимости ряда: 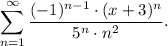
Другие вопросы по теме Алгебра
Популярные вопросы
- Кто главные герои книги драгунский.в динискины рассказы. рассказ друг...
2 - Есимнен етистик тудыратын журнактар...
2 - Третий и пятый члены прогрессии равны12 и 48, найти восьмой член...
3 - Из-за чего началась японская война ?...
1 - Запиши четыре составных количественных числительных и четыре составных...
2 - 1. i am going to play football. 2. they are going to take a number...
2 - Пересказ рассказа макар чудра (своими словами) и персонажей разделить...
3 - Емкость конденсатора в колебательном контуре равна 50 мкф. зависимость...
2 - Процесс отдачи электронов окисление изомеризация восстановление разложение...
1 - Вкаком из предложений пропущена одна (только одна! ) запятая? 1) впрочем,...
2
Объяснение:
Значит, ряд сходится в области, удовлетворяющей неравенству
Исследуем сходимость на концах интервала.
1)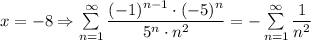 - сходится как обобщенный гармонический ряд с
- сходится как обобщенный гармонический ряд с 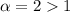
2)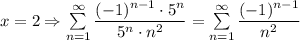 - согласно пункту 1) ряд из модулей сходится, а значит данный ряд сходится абсолютно.
- согласно пункту 1) ряд из модулей сходится, а значит данный ряд сходится абсолютно.