Найти область определения функции y=6-x/3x+1 решить уравнение 2sinx-cos^2x*sinx=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Знайти добуток значень x та y, які є розв’язком системи рівнянь...
2 - Який з океанів більший за площею?...
2 - Укажи, какие утверждения относятся к Молекулярно-Кинетической Теории строения...
1 - довжина сторони ромба дорівнює 5 см Одна з діагоналей довша за іншу на...
1 - Bir yigit bn qiz yaxshi ko rishadi.Ular qishda uchrashishadi.hammayoq qor...
2 - Решите иррациональное неравенство ...
1 - На дне водоема глубиной 80 см находится точечный источник света. Если показатель...
3 - Решить уравнение. Заранее благодарю! log2x(x−1)=2...
3 - В геометричной прогресии (bn) B3 = 24, q= -2. Найти B1. :)...
2 - Найдите все такие простые p, что p²+14-тоже простое...
1
I.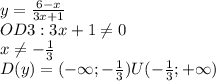
II. 2sinx-cos^2x*sinx=0
sinx(2-cos^2x)=0
1)sinx=0
x=pik . k=z
2)2-cos^2x=0
cos^2x=2
cosx=+-√2
x=+-arccos(+-√2)+2pik . k=z
2sinx-cos^2x*sinx=0
sinx(2-cos^2x)=0
1)sinx=0
x=πk, k∈Z
2)2-cos^2x=0
cos^2x=2
cosx=±√2
x=±arccos(±√2)+2πk, k∈Z