Найти область определения функции x-4 / ln (x^2 + 5x - 14)
Другие вопросы по теме Алгебра
Популярные вопросы
- Яка максимальна довжина хвилі електромагнітного випромінювання, що може викликати...
2 - Двухосновной кислородсодержащей кислотой является? А) H3PO4В) H2SO3Б)HNO3Г) HCl...
3 - Розв’яжіть нерівність 0, 2(7- 2x ) ≥ 2,3- 0,3(x −6)....
3 - 1. Составьте алгоритм учета выручки 2. Составьте алгоритм учета с поставщиками...
1 - Сөйлемді толықтыр керекті сөздерді жаз.1.Энштейн жаңғалақ , салды-салдыр болға...
2 - В 1 только последние а во 2 всё пожайлуста...
1 - НУЖНО! Познач речення з однорідними членами. Постав розділові знаки. •Від добра...
2 - Гурт творчість якого стала початком рок-музики охопивши практично весь світ...
3 - ) НаДО решить 3 задачи по математике. 1. АА1 - перпендикуляр к плоскости, АВ...
3 - Стислий письмовий переказ ,,Усмішка Рей Бредбері Чим найшвидше HELP ME PLEAS...
3
Объяснение:
ОДЗ:
-∞__+__-7__-__2__+__+∞
ответ: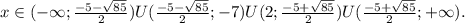
ответ на фото закреплён