1. Алгебра
  2. Найти область определения

Найти область определения функции 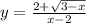y = \frac{2 + \sqrt{3 - x} }{x - 2}

с объяснением
ответ должен быть (-бесконечность;2) и (2;3]​

dbjshsg dbjshsg    2   28.06.2021 11:26    0

Ответы
alinamironova21 alinamironova21  28.07.2021 11:26

(-∞; 2)∪(2; 3]

Объяснение:

Ограничения в область определения функции вносят деление, которое на ноль не имеет смысла, и квадратный корень, который можно извлекать лишь из неотрицательных чисел (на множестве ℝ). Получили систему:

\begin{cases} x-2 \ne 0 \\ 3-x\geq 0 \end{cases}\\ \begin{cases} x \ne 2 \\ x\leq 3 \end{cases}\\\begin{cases} x \ne 2 \\ x \in (-\infty;3] \end{cases}

Найдем пересечение и запишем ответ в виде объединения числовых промежутков:

D(f)=(-\infty; 2)\cup(2;+3]

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
оскар4444 оскар4444  20.05.2019 17:50
Впрогрессии b5=81, q=3/4 найдите: а)первый член прогресии б)сумму первых пяти членов в)запишите формулу n-го члена этой прогрессии...
riblika11 riblika11  20.05.2019 17:50
Путь в 195км путешественники проплыли, двигаясь 3ч на моторной лодке и 5ч-на пароходе. какова скорость лодки, если она вдвое меньше скорости парохода?...
ksenia376 ksenia376  20.05.2019 17:50
Найдите первый член и разность арифметической прогрессии, в которой s4=-4 и s7=8...
Ihalina Ihalina  20.05.2019 17:50
Решите уравнение 1+7+13++x=280 тема арифметические и прогрессии...
резной777 резной777  20.05.2019 17:50
решения 9y-8x=89 -8x-9y=-73 это в скобках кто может...
hamaturov hamaturov  20.05.2019 17:50
Ришитесистему неравенств 7-х ≤ 1-4х 18+2х -3-5х...
Akbota0504 Akbota0504  20.05.2019 17:50
Сколько существует трехзначных чисел с суммой цифр 8? пусть abc - некое трехзначное число. может ли сумма abc+bca+cab быть полным квадратом. два , желательны объяснения....
Yarik176 Yarik176  20.05.2019 17:50
Log по основанию a от x =2log по основанию a от 3 + log по основанию а от 5...
zholdashev zholdashev  20.05.2019 17:50
Решите неравенство: а)1-3х 0 б)3х-2 3-х в)5(y-1,2)-4,6 3y+1...
23414262 23414262  20.05.2019 17:50
Log по основанию 0.3 (5+2х)=1 прологарифмировать.предложения?...

Популярные вопросы