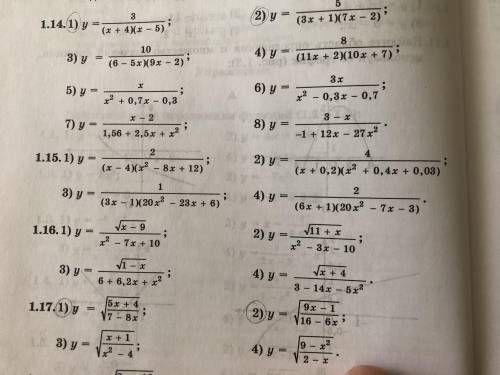
Алгебра: найти область определения функции (4) пример. Номер 1.15

найти область определения функции (4) пример. Номер 1.15

Ответы

Hitecho07 25.11.2021 09:30

Область определения функции (D(y)) -- это все значения x, при которых функция (выражение, которым она задана) существует.

Во всех пунктах представлена дробь, где переменная только в знаменателе.

Дробное выражение существует, если знаменатель не обращается в ноль.

Нужно найти значения x, при которых знаменатель обращается в ноль и исключить их из области определения.

$1)\;\;y=\dfrac{2}{(x-4)(x^2-8x+12)} \\ \\(x-4)(x^2-8x+12)=0\\ \\ x-4=0\\ (x-6)(x-2)=0 \\ \\ x=4\\x=6\\x=2\\\\D(y)=(-\infty;2)\cup(2;4)\cup(4;6)\cup(6;+\infty)\\ \\ 2)\;\;y=\dfrac{4}{(x+0,2)(x^2+0,4x+0,03)} \\ \\(x+0,2)(x^2+0,4x+0,03)=0\\ \\ x+0,2=0 \\(x+0,03)(x+0,01)=0\\ \\x=-0,2\\x=-0,03\\x=-0,01\\\\D(y)=(-\infty;-0,2)\cup(-0,2;-0,03)\cup(-0,03;-0,01)\cup(-0,01;+\infty)$

$3)\;\;y=\dfrac{1}{(3x-1)(20x^2-23x+6)} \\ \\(3x-1)(20x^2-23x+6)=0\\ \\ 3x-1=0\quad \Rightarrow \quad x_1=\dfrac{1}{3} \\\\ 20x^2-23x+6=0 \\\\D=23^2-4\cdot20\cdot6=529-480=49\\\\x_2=\dfrac{23-\sqrt{49}}{40}=\dfrac{2}{5} \\\\x_3=\dfrac{23+\sqrt{49}}{40}=\dfrac{3}{4} \\\\D(y)=(-\infty;\dfrac{1}{3})\cup(\dfrac{1}{3};\dfrac{2}{5} )\cup(\dfrac{2}{5} ;\dfrac{3}{4})\cup(\dfrac{3}{4};+\infty)$

$4)\;\;y=\dfrac{2}{(6x+1)(20x^2-7x-3)} \\ \\(6x+1)(20x^2-7x-3)=0\\ \\ 6x+1=0\quad \Rightarrow \quad x_1=-\dfrac{1}{6} \\\\ 20x^2-7x-3=0 \\\\D=7^2-4\cdot20\cdot(-3)=49+240=289\\\\x_2=\dfrac{7-\sqrt{289}}{40}=-\dfrac{1}{4} \\\\x_3=\dfrac{7+\sqrt{289}}{40}=\dfrac{3}{5} \\\\D(y)=(-\infty;-\dfrac{1}{4})\cup(-\dfrac{1}{4};-\dfrac{1}{6} )\cup(-\dfrac{1}{6} ;\dfrac{3}{5})\cup(\dfrac{3}{5};+\infty)$