Найти неопределенный интеграл
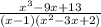
Другие вопросы по теме Алгебра
Популярные вопросы
- Скольки равняется нормальное атмосферное давление ?...
2 - Построить график функции y=kx+b если известно что он проходит через точку m(2;...
2 - Были отменены самые жестокие полей были было рабство, отпускались на волю, рабами...
1 - Вравнобедреной трапепеции меньшее основание равно 4см,боковая сторона 6см,а один...
3 - Х-3,8 = - 4,75 и 5 13/35 +х = -2 13/14 решите уровнение...
3 - Решить: 687,8+(8,0802-85,3712): 0,045+3,5: 70-7: 3,5...
3 - Диагональ bo параллелограмма abcd перпендикулярна к стороне ad, ab=10cм, угола=14градусов...
2 - Как решить эту ? на поливку клумбы израсходовали 3 ведра воды, по 6 л в каждом....
2 - Найдите значение выражения корень 343/корень 7...
3 - Cоставь и запиши связный текст ( из 4 предлжений ) о выращивании хлеба используя...
3
Разделим числитель на знаменатель:
первый интеграл:
второй интеграл:
с неопределенных коэффициентов разделим на простейшие дроби:
получаем:
складываем ответы первого и второго интегралов получаем: