Найти неопределенный интеграл
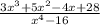
Другие вопросы по теме Алгебра
Популярные вопросы
- Купили 5кг муки. израсходовали 3/5 этого количества. сколько граммов...
3 - Що мене зачепило у творі три як рідні брати ?...
2 - На пошив потратили 1/3 и 1/6 м.ткани.осталось 460 м. сколько всего было...
2 - Если к четырём последовательным членам арифметической прогрессии прибавить...
3 - Запасы воды на земле сост примерно 1359 млн.м3. из этого кол-во в океанах...
1 - Кольчатые черви – это наиболее высокоорганизованные животные среди других...
1 - Что больше? а) 8000 бит б)1001 байт в)1 кбайт г) 0.001 мбайт...
2 - Замените словосочетание любил танцевать построенное на основе примыкания,...
3 - Муравей со штангой весит 16 г. какова масса муравья, если он в 7 раз...
2 - Сочинение про морскую свинку на (если можете потом ещё на , что вы там...
3
Раскладываем на простейшие дроби с неопределенных коэффициентов:
система:
получаем:
-------------------------