Найти наименьшее значение функции на промежутке [-1;1]
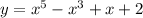
Другие вопросы по теме Алгебра
Популярные вопросы
- 31. скорость легкового автомобиля в 2 раза больше скорости грузового,...
2 - Тема: циклические алгоритмы; даны числа на отрезке от -5 до 5. найти...
2 - Дано трапеция abcd ab паралельно cd найти ab если od = 15см ob=9см...
2 - Умоляю , последние . органика 10 класс стрелкой 1500 градусов, как...
3 - Это нормально вообще, так нервничать, когда тебе двадцать три года,...
3 - Перетворення води в природі з одного стану в інший називається...
3 - Составьте 5 предложений с бiрiккен соз это слова пишущиеся слитно...
3 - Завершите предложения с глаголами в скобках. my name s eric and i...
3 - Как поделить на слоги слово с предлогом о вопль?...
1 - Решите уравнения: x^2-121=0 x^2+26x+169=0 x^2-28x+169=0 x^5-16x=0...
1
у = х⁵ - х^3 + х + 2;
Найдём производную :
у' = (x⁵)' - (x³)' + x' + 2' = 5х⁴ - 3х^2 + 1;
5х⁴ - 3х^2 + 1 = 0;
x² = m , m ≥ 0
5m² - 3m + 1 = 0
D = 3² - 4 * 5 = 9 - 20 = -11 < 0.
Действительных корней нет .
Первый коэффициент больше нуля, значит, производная положительна, и функция возрастает. Для возрастающей функции наименьшее значение на заданном отрезке [-1; 1] будет на левом, а наибольшее значение - на правом конце:
min(y) = y(-1) = (-1)⁵ - (-1)³ - 1 + 2 = -1 + 1 - 1 + 2 = 1