1. Алгебра
  2. Найти наибольшую площадь

Найти наибольшую площадь ромба, сумма длин диагоналей которого равна 12 см (с решением)

ama14 ama14    3   16.09.2019 14:50    86

Ответы
Настя9474 Настя9474  07.10.2020 19:56

Пусть диагонали ромба равны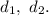 d_1,~ d_2. Площадь ромба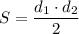 S=\dfrac{d_1\cdot d_2}{2}

Для положительных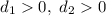 d_10,~ d_20 применим неравенство Коши

d_1+d_2\geq 2\sqrt{d_1d_2}\\ \\ \sqrt{d_1d_2}\leq 6\\ \\ d_1d_2\leq 36

И это неравенство достигает максимума при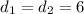 d_1=d_2=6 см.

Наибольшая площадь: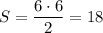 S=\dfrac{6\cdot 6}{2}=18 см²

По условию,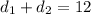 d_1+d_2=12 откуда 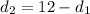d_2=12-d_1. Рассмотрим функцию: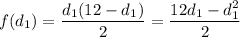 f(d_1)=\dfrac{d_1(12-d_1)}{2}=\dfrac{12d_1-d_1^2}{2}

Графиком функции есть парабола, ветви которой направлены вниз. Вершина параболы достигает максимума.

d_1=-\dfrac{b}{2a}=\dfrac{12/2}{2\cdot 1/2}=6 см

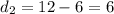Тогда d_2=12-6=6 см

Площадь S = 18 см²

ответ: 18 см²

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
zvon007 zvon007  06.10.2019 11:40
Решить 2 примера, (х-1)^2=2х-2х^2 и 1/4х^2-1/2х=0 , пож...
Katranov2016 Katranov2016  06.10.2019 11:40
Найдите наибольшее значение выражения 1-(cos^2α-sin^2α) , 1-sinα*cosα*tgα , sinα+3sin^2α+3cos^2α...
semabulov semabulov  06.10.2019 11:40
Представте в виде куба двучлена многочлены1) а^3-6а^2в+12ав^2-8в^3...
Slysly Slysly  06.10.2019 11:40
Найдите наибольший объем треугольной пирамиды mabc, в основании которой лежит равнобедренный треугольник abc (ab=bc), если мв перпендикулярна abc и ma=√3...
dog12361246 dog12361246  06.10.2019 11:40
Периметр прямоугольника равен 32 см ,а сумма площадей квадратов, построенных на двух его соседних сторонах,-130 см кв.найдите стороны прямоугольника....
AndreiBrazhnikov1 AndreiBrazhnikov1  06.10.2019 11:40
Замени m одночленом так, чтобы получился квадрат бинома 64x^2−5x+m m=...
Polikaza Polikaza  06.10.2019 11:40
Из одного города в другой,расстояние между которыми равно 240 км,выехали одновременно автобус и машина.автобус прибыл в пункт назначения на 1 час позже машины.найдите скорость...
anastasijamak anastasijamak  18.02.2021 06:55
Решите уравнения (1, 2) 7 класс.​...
hetag15 hetag15  18.02.2021 06:53
Решите уравнение:x²+4x-21=0...
kmatachp01gzm kmatachp01gzm  18.02.2021 06:53
Медианы ВН, СК и AD треугольника АВС пересекаются в точке 0 , площадь ABC =60 cm². Найди площадь BOD если можно с рисунком...

Популярные вопросы