Найти наибольший отрицательный корень уравнения: √3*sin(x/6)+cos(x/6)=√2
Ответы
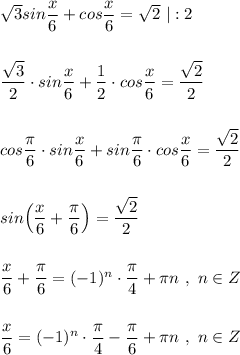
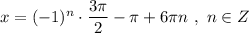
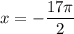 - наибольший отрицательный корень уравнения
- наибольший отрицательный корень уравнения
Другие вопросы по теме Алгебра
Популярные вопросы
- дати відповідь на запитання чому ангел такий маленький та чому лев...
2 - Знайдіть відстань між точками А(2;3) і В(5;7)...
1 - Узгодження Часів Його мама сказала, що вона працює в цій лікарні.2....
2 - 2 - x - 4x ^ 4 = 0 какое это уравнение?...
2 - Афоризмы о законе, в произведении Н.С.Лескова Старый гений...
3 - Есть два провода из одинакового вещества и одинаковой длины. Y одного...
2 - Синквей на тему Архетектурна руси...
2 - УС ә) Ауылдан калаға дейін 340 км. Ауылдан калага мотоциклі 4 кмжылдамдықпен...
1 - тему не понял, а тест важный и нужно сдать:(...
3 - Радіоприймач налаштовували на приймання втричі довшиз хвиль. Як...
1