Найти наибольшее и наименьшее значения функции 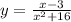 на отрезке [-5; 5]
на отрезке [-5; 5]
Другие вопросы по теме Алгебра
Популярные вопросы
- Сочинение на тему зима чтобы было на всю страницу !...
3 - 20 ,только решение а не ответ две стороны треугольника равны...
1 - Перевисти текст с казахского жас өспірімге спорттық үлгімен...
2 - Рассказ о том как капля воды может жизнь человека...
1 - 918 саны мен 9 жане 2 сандары кобейтиндисинин айырмасы...
3 - Сочинение на тему урожай . 7-8 предложений...
1 - Какие из данных множеств являются пустыми? 1)множество учащихся...
2 - Изучить, , светить, танцевать, торопиться, обещать какие из...
3 - Кто проявляет агрессию по отношению к донбассу (атакует его)...
2 - ответьте на вопросы: әңгімелесіп отырған ңды бар ынтаңмен тыңдай...
2
Решение.