1. Алгебра
  2. Найти наибольшее и наименьшее

Найти наибольшее и наименьшее значение функции y= - 16/3 * x^(3/2) + 1/3 *x^3 на промежутке [1; 9]

ЭтоКтоТо ЭтоКтоТо    1   07.07.2019 20:10    6

Ответы
2001snk 2001snk  30.07.2020 23:18

y = -\dfrac{16}{3} x^{\frac{3}{2}} + \dfrac{1}{3} x^3

Степенная функция с рациональным показателем степени определена при х > 0.


y'=(-\dfrac{16}{3} x^{\frac{3}{2}})' + (\dfrac{1}{3} x^3)'=-\dfrac{16}{3}*\dfrac{3}{2} x^{\frac{1}{2}} + \dfrac{1}{3}*3 x^2 =\\ \\ =-8x^\frac{1}{2} +x^2 =x^2-8x^{\frac{1}{2}} =x^\frac{1}{2} (x^\frac{3}{2} - 8)


В точках локальных экстремумов первая производная равна нулю.

y'=x^\frac{1}{2} (x^\frac{3}{2} - 8)=0\\ \\ 1) x^\frac{1}{2} =0; x_1 = 0\\ \\ 2) x^\frac{3}{2} - 8=0; (\sqrt{x} )^3=2^3;\sqrt{x} =2; x_2=4

Точка x₁ = 0 в промежуток [1; 9] не попадает.


Чтобы найти наименьшее и наибольшее значение функции на интервале, нужно вычислить значение функции в точках экстремумов и на концах интервала.

x=1; y = -\dfrac{16}{3}* 1^{\frac{3}{2}} + \dfrac{1}{3}* 1^3=-\dfrac{16}{3} +\dfrac{1}{3} =-5\\ \\ x=4; y = -\dfrac{16}{3}* 4^{\frac{3}{2}} + \dfrac{1}{3}* 4^3=-\dfrac{16*8}{3} +\dfrac{64}{3} =-21\dfrac{1}{3} \\ \\ x=9;y = -\dfrac{16}{3}* 9^{\frac{3}{2}} + \dfrac{1}{3} *9^3=-\dfrac{16*3^3}{3} + \dfrac{3^6}{3}=-144+243=99


ответ: наименьшее значение функции f(4) =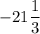 -21\dfrac{1}{3};

            наибольшее значение функции f(9) = 99

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Dashacolod Dashacolod  28.04.2020 08:20
1. Позвольте x(n) обозначить количество положительных целых делителей n . Найдите сумму шести наименее положительных целых чисел, которые являются решениями x(n)+x​...
Соня11647 Соня11647  28.04.2020 08:20
Докажите что при всех допустимых значениях y значение выражение не зависит от y a) 5y+3/2y+2-7y+4/3y+3b)11y+13/3y-3+15y+17/4-4y​...
Nutmi Nutmi  28.04.2020 08:20
Tg 22 + tg 23 1 - tg 22 tg 23. найдите значение выражения​...
dog126 dog126  28.04.2020 08:20
Пересекает ли график функции ось x, и если пересекает, то в каких точках: y=x^2-x+12 с объяснениями!...
плвлаовг плвлаовг  28.04.2020 08:20
Решите системы уравнений графическим методом...
ArtGame23 ArtGame23  28.04.2020 07:40
2. Выполните умножениеа) (2a+b)(2a-b)б) (4х+1) (16x²-4х+1)​...
RusskikhDaria RusskikhDaria  28.04.2020 06:36
Разложите на множители 4-4^3/4; (2а)^1/2-(5а...
vaselzhiriy vaselzhiriy  28.04.2020 06:36
Найди значение , соответствующее значению =0 для линейного уравнения 15+17=75....
0508761681 0508761681  22.04.2020 13:58
Какова вероятность того,что наугад выбранное делителем числа 210 окажется числом?​...
ŦáêHŷùnģ ŦáêHŷùnģ  22.04.2020 13:58
Телефонная станция обслуживает абонентов , у которых номера телефонов состоят из семи цифр и начинаются с 218 . На сколько абонентов рассчитана эта станция?...

Популярные вопросы