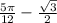Найти наибольшее и наименьшее значение функции на отрезке
Другие вопросы по теме Алгебра
Популярные вопросы
- Является ли пара чисел ( 4; -1) решением системы уравнений: 2x+3y=5 x-2y=6...
1 - Определите атмосферное давление на вершине горы высоты 3000м если у подножья оно...
2 - Дана арифметическая прогрессия (-4, -1, найдите сумму первых шести её членов...
3 - При взаимодействии с водой образует щёлочь 1) k2o 2) al2o3 3) co2 4) cuo...
2 - Вычислить: сos альфа,sin 2 альфа,если сtg альфа =корень из 7. п...
2 - Сколько граммов гидроксида натрия потребуется для нейтрализации 200см3 серной кислоты...
3 - Углы δ относятся как 1: 1: 1. определите вид данного δ. по углам: по сторонам:...
1 - Польский исследователь а.фидлер писал, что бразильская сельва может вызвать чувство...
3 - (4x+3)(3-4x)+(3x-4)в квадрате - (19-16x) )...
2 - Сообщение занимает 3 страницы по 25 строк. в каждой строке записано по 60 символов....
2
Найти наибольшее и наименьшее значение функции на отрезке
y = x/2 + cos(x), x ∈ [0;π].
Найдем производную данной функции
И приравняем ее к нулю.
Корни удовлетворяющие отрезку [0;π/6] : π/6 и 5π/6
Найдем наименьшее и наибольшее значение функции на концах отрезка.
Наибольшее значение функции равно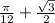 , а наименьшее
, а наименьшее