Найти множество значений функции 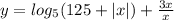
при
x = > - 125
Другие вопросы по теме Алгебра
Популярные вопросы
- Доля жінки в повісті ольги кобилянської людина напишіть твір ...
1 - 10 класс с «заряженный шарик массой m висит на нити длиной i. когда под ним на расстоянии...
3 - Перевести. at the circus this is a circus.you can see trained animals on the ring.the...
2 - Сократите аллергическую дробь...
2 - 8) 3/4 : (1/2 - 2/5) + (3/4 + 5/6) : 1/6 9) (2/15 + 7/12) x 30/43 + 2 : 1/2 10)...
3 - 1. следующие устойчивые выражения относятся к стилю: 1)бить баклуши, ножки буша...
1 - За якою формулою обчисляють тиск стовпа рідини? ...
3 - Выберите цитаты выражающие негативное отношение автора к действительности собачье...
3 - Var s, n : longint; begin s : = -1; n : = 3; while 6*s*s*s*s*s 800*s*s*s do begin...
2 - Сделать краткое сообщение по (8 класс)на тему: магнитное поле в солнечном системе...
2
y > 6
Объяснение:
Если x ≥ -125, то есть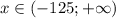 , то
, то 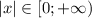 , но так как x стоит в знаменателе дроби, он не может быть равен нулю. Получаем
, но так как x стоит в знаменателе дроби, он не может быть равен нулю. Получаем