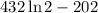Найти максимум функции y=x^2-34x+144lnx+6
Другие вопросы по теме Алгебра
Популярные вопросы
- Тарас бульба. сочинение про мать андрея и остапа.(сказали должно быть...
2 - Анализ стихотворения а.с.пушкина дар напрасный, дар случайный средства...
2 - Чему равен коэффициент одночлена а5вс5. 4. чему равна степень одночлена...
3 - На подоконнике окна с двойными рамами стоит ваза. вечером из комнаты...
2 - Как расположены листья на стебле у розоцветных...
3 - Кто главные герои рассказа бирюк тургенев? !...
3 - Перевод текста we were a company of young englishmen and one day our...
3 - Врезультате какой реакции из этилена можно получить ацетилен: гидратации...
2 - Запишите смешанное число в виде неправильной дроби 2 4/5; 6 7/11; 12...
1 - При каких значениях b уравнение x²+bx+4=0; 1)имеет два корня , один...
3
Найдём производную функции:
Посмотрим, как ведёт себя функция (см. рис.). Видно, что возрастание сменяется убыванием в точке x = 8. Значение в точке максимума: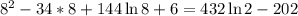
ответ: