Алгебра: Найти корни уравнения! [tex]x^3-6x^2+6x-2=0[/tex]

Докажем сначала, что корень единственный. Для этого исследуем функцию корни производной В точке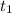 функция имеет локальный максимум, в точке 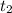- локальный минимум, после него функция монотонно растет. так как корень из двух меньше, чем 1,5. Итак, слева от функция возрастает, справа убывает, начиная с снова возрастает. Поскольку функция в точке отрицательна, существует только один корень функции (и расположен он правее ; для нас, правда, важна только его единственность).Возвращаемся к уравнению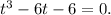 Для его...

Найти корни уравнения! $x^3-6x^2+6x-2=0$

Ответы

ffjrppyegxvhd 23.06.2020 10:59

$x^3-6x^2+6x-2=0;\ (x^3-3 x^2\cdot 2+3x\cdot 2^2-2^3)-6x+6=0;$

$(x-2)^3-6(x-2)-6=0;\ x-2=t;\ t^3-6t-6=0.$

Докажем сначала, что корень единственный. Для этого исследуем функцию y=t^3-6t-6.

y'=3t^2-6; корни производной $t_1=-\sqrt{2}; t_2=\sqrt{2}.$

В точке t_1 функция имеет локальный максимум, в точке t_2 - локальный минимум, после него функция монотонно растет.

$y(-\sqrt{2})=-2\sqrt{2}+6\sqrt{2}-6=2(2\sqrt{2}-3)<0,$ так как корень из двух меньше, чем 1,5. Итак, слева от t_1 функция возрастает, справа убывает, начиная с t_2 снова возрастает. Поскольку функция в точке t_1 отрицательна, существует только один корень функции (и расположен он правее t_2 ; для нас, правда, важна только его единственность).

Возвращаемся к уравнению t^3-6t-6=0. Для его решения применим метод Кардано. Замена 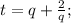$t=q+\frac{2}{q};$ после элементарных упрощений получаем уравнение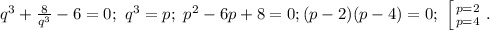 $q^3+\frac{8}{q^3}-6=0;\ q^3=p;\ p^2-6p+8=0; (p-2)(p-4)=0;\ \left [ {{p=2} \atop {p=4}} \right. .$

Вроде бы надо исследовать оба значения p, однако оба они дадут одно и то же значение t (кстати, ранее мы даже доказали, что двух решений быть не может). Итак, пусть p=2; $q=\sqrt[3]{2};\ t=\sqrt[3]{2}+\frac{2}{\sqrt[3]{2}}=\sqrt[3]{2}+\sqrt[3]{4}; x=2+\sqrt[3]{2}+\sqrt[3]{4}$