Найти корни уравнения, принадлежащие интервалу. То есть, сначала надо решить уравнение, а потом отобрать корни. Уравнение в прикреплённом файле.
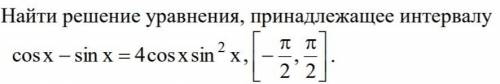
Ответы
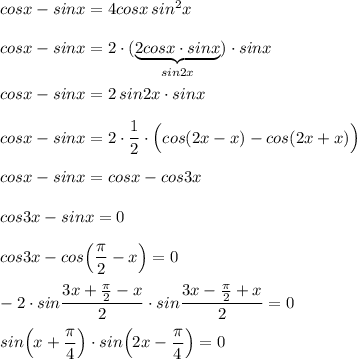
![\displaystyle a)\ \sin\Big(x+\dfrac{\pi }{4}\Big)=0\ \ ,\ \ x+\frac{\pi}{4}=\pi n\ \ ,\ \ x=-\frac{\pi}{4}+\pi n\ ,\ n\in Z\\\\b)\ \ sin\Big(2x-\dfrac{\pi}{4}\Big)=0\ \ ,\ \ 2x-\frac{\pi}{4}=\pi k\ \ ,\ \ 2x=\frac{\pi}{4}+\pi k\ \ ,\ \ x=\frac{\pi}{8}+\frac{\pi k}{2}\ ,\ k\in Z\\\\c)\ \ x\in \Big[-\frac{\pi }{2}\, ;\ \frac{\pi }{2}\ \Big]:\ x=-\frac{3\pi}{8}\ ,\ -\frac{\pi}{4}\ ,\ \frac{\pi }{8}\ .\\\\\\Otvet:\ \ a)\ \ x=-\frac{\pi}{4}+\pi n\ ,\ \ x=\frac{\pi}{8}+\frac{\pi k}{2}\ ,\ \ n,k\in Z\ ;](/tpl/images/2055/8243/a733c.png)
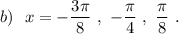
Другие вопросы по теме Алгебра
Популярные вопросы
- Дано ab=bc dm перпендикулярен ac, en перпендикулярен ac,am=nc доказать...
2 - При___-распаде одного химического элемента образуется другой химический...
3 - Расстрепанный воробе что правда и вымысел не понимаю....
3 - RMNECHIEKA что за профессия на немецком из этих букв...
1 - Как можно рассчитать величину индукционного тока, возникающего в...
2 - I вариант. I. Вместо пропусков вставьте глаголы can, may или must....
2 - беремiн. (толык жауап керек)6 тапсырма...
3 - Отзыв на произв. Ю. Кузнецовой ангела...
3 - Напишите правильный вариант оборота to be going to в данном предложении....
1 - При каком короле в Англии началось формирование абсолютной монархии?...
1