1. Алгебра
  2. Найти корни квадратного трехчлена:

Найти корни квадратного трехчлена: №1. а.) 6х в квадрате +5х-4 б.) 3х в квадрате -2х-8 разложить на множители квадратный трехчлен: а) -х в квадрате +9х-8 б) 1х в квадрате +х -6 - 3 в) -х в квадрате +4х-3 г) 1х в квадрате -2х-6 - 2

НиколайКот НиколайКот    3   01.03.2019 06:50    6

Ответы
angelinochka345 angelinochka345  23.05.2020 17:55

№1

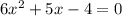
а)6x^{2}+5x-4=0

Cчитаем дискриминант:

D=5^{2}-4\cdot6\cdot(-4)=25+96=121

Дискриминант положительный

\sqrt{D}=11

Уравнение имеет два различных корня:

x_{1}=\frac{-5+11}{2\cdot6}=\frac{6}{12}=\frac{1}{2}=0,5

x_{2}=\frac{-5-11}{2\cdot6}=\frac{16}{12}=\frac{4}{3}=1\frac{1}{3}

 

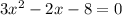
б) 3x^{2}-2x-8=0

Cчитаем дискриминант:

D=(-2)^{2}-4\cdot3\cdot(-8)=4+96=100

Дискриминант положительный

\sqrt{D}=10

Уравнение имеет два различных корня:

x_{1}=\frac{2+10}{2\cdot3}=\frac{12}{6}=2

x_{2}=\frac{2-10}{2\cdot3}=\frac{-8}{6}=-\frac{4}{3}=-1\frac{1}{3}

 

№ 2

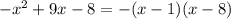
а) -x^{2}+9x-8=-(x-1)(x-8)

для того чтобы разложить квадратный трёхчлен нужно приравнять его к нулю и найти корни уравнения

-x^{2}+9x-8=0

Cчитаем дискриминант:

D=9^{2}-4\cdot(-1)\cdot(-8)=81-32=49

Дискриминант положительный

\sqrt{D}=7

Уравнение имеет два различных корня:

x_{1}=\frac{-9+7}{2\cdot(-1)}=\frac{-2}{-2}=1

x_{2}=\frac{-9-7}{2\cdot(-1)}=\frac{-16}{-2}=8

 

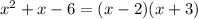
б) x^{2}+x-6=(x-2)(x+3)

делаем всё по аналогии

x^{2}+x-6=0

Cчитаем дискриминант:

D=1^{2}-4\cdot1\cdot(-6)=1+24=24

Дискриминант положительный

\sqrt{D}=5

Уравнение имеет два различных корня:

x_{1}=\frac{-1+5}{2\cdot1}=\frac{4}{2}=2

x_{2}=\frac{-1-5}{2\cdot1}=\frac{-6}{2}=-3

 

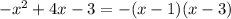
в) -x^{2}+4x-3=-(x-1)(x-3)

делаем всё по аналогии

-x^{2}+4x-3=0

Cчитаем дискриминант:

D=4^{2}-4\cdot(-1)\cdot(-3)=16-12=4

Дискриминант положительный

\sqrt{D}=2

Уравнение имеет два различных корня:

x_{1}=\frac{-4+2}{2\cdot(-1)}=\frac{-2}{-2}=1

x_{2}=\frac{-4-2}{2\cdot(-1)}=\frac{-6}{-2}=3

 

г) x^{2}-2x-6-2=x^{2}-2x+(-6-2)=x^{2}-2x-8=(x-4)(x+2)

делаем всё по аналогии

x^{2}-2x-8=0

Cчитаем дискриминант:

D=(-2)^{2}-4\cdot1\cdot(-8)=4+32=36

Дискриминант положительный

\sqrt{D}=6

Уравнение имеет два различных корня:

x_{1}=\frac{2+6}{2\cdot1}=\frac{8}{2}=4

x_{2}=\frac{2-6}{2\cdot1}=\frac{-4}{2}=-2

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Qwertyuio111 Qwertyuio111  01.09.2019 18:00
2корень из3-х = х-1 (решить уравнение)...
Гавхарчик Гавхарчик  01.09.2019 18:00
1) p^2 + 4q^2-9r^2-4pq; 2) (m+2n)^3-m^2-4mn-4n^2...
mi1980 mi1980  01.09.2019 18:00
Дана функция f(x)=-3x+2. найдите наименьшее целое число x, при котором значение функций f меньше 6....
12345678006432 12345678006432  01.09.2019 17:50
1(x+3)(x--4)(x+4)=11 найдите корень уравнения 2 {x-y=3, 2x-3y=4. решите систему уравнений 3 за 5 кг конфет и 4 кг печенья заплатили 320грн. сколько стоит 1 кг конфет...
Dan1la1 Dan1la1  01.09.2019 17:50
Решить sin90-sin(-45) 2? 2sin60+cos(-90) 2...
karina36517 karina36517  01.09.2019 17:50
Решить неравенства (2+√3)(1-√3)+√3...
NikkiLee NikkiLee  01.09.2019 17:50
Решить 9класс sin45°+cos(45°) 1 tg30°-tg(60°) 1...
марс55 марс55  01.09.2019 17:50
Разложите на множители выражение 3(а+в)^2-ху(а+в)...
18alinochka150 18alinochka150  01.09.2019 17:50
Укажите наибольшее из следующих чисел: 3√11; 10; √101; 7√2; (с решением, )...
NAPAS228 NAPAS228  01.09.2019 17:50
Дано вектори a→(3; −1)a→(3; −1) і b→(1; −2)b→(1; −2). знайдіть координати вектора m→m→, якщо m→=3a→−2b→m→=3a→−2b→...

Популярные вопросы