Найти интегралы методом замены переменной 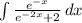
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему от донора риципиенту можно перелевать кровь,совместимую по группе...
3 - Какую продукцию выпускали на петровских заводах?...
2 - :в одном мешке в три раза меньше крупы чем во втором а в третьем на...
3 - (2 ) из строк 17-24 выпишите имена существительные, имеющие нехарактерные...
3 - Дана функция y=0.5x-1 составьте таблицу значений в точках -1; 0; 1;...
1 - Найдите меньший угол равнобедренной трапеции, если два ее угла относятся...
3 - Вновелле ,,золотой жук не рассказывается о капитане килде, придумайте...
1 - При постоянном давлении 10^5 па объем воздуха находившейся в квартире...
2 - Имеет ли решение уравнение : √х-1+√х+1+1=0 , х-1 и х+1 они полностью...
2 - Валентин подарил виктории розы и орхидеи,причём орхидей было в 4 раза...
3
Решение приложено...
Объяснение:
Делаем замену
Тогда интеграл запишется, как