Найти интеграл
(10х^2-16х)/(х^3-6х^2+16х-16)
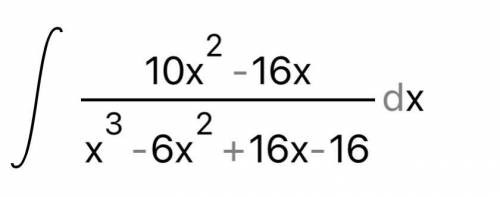
Другие вопросы по теме Алгебра
Популярные вопросы
- Спортивная площадка площадью 1200 м2 имеет форму прямоугольника, ширина которого...
3 - Исправьте предложение: труд представляет собой своеобразный вид их деятельности...
2 - Составте вопросительные предложения...
3 - Доведіть що тополя тараса шевченка - . , !...
3 - Отзыв о комедии н.г.гоголь «ревизор»...
2 - Ятут должна сделать своему брату 25 поводов сказать ! так вот что мне написать...
2 - Найди значение выражения с+7 с-8 при с=9 с=22 с=90...
1 - Из полной бочки взяли 14,4 кг квашеной капусты и затем еще 5/12 этого количества...
1 - Начертите прямоугольник abcd соедините отрезком вершины a и c найдите площади...
3 - Найти правильные и не правильные глаголы a town mouse and a country mouse were...
1
делим на простейшие дроби с неопределенных коэффициентов:
получаем:
первый интеграл
второй интеграл
делаем в числителе производную знаменателя:
(х^2-4х+8)'= 2х-4
Получаем: