Найти два положительных числа, одно число больше другого на 5, произведение равно 24

Представим первое число как X

Второе как X + 5

Составим уравнение и решим его.

x * (x+5) = 24

x² + 5x = 24

x² + 5x - 24 = 0

(a = 1; b = 5; c = -24.)

D = b² - 4ac

D = 5² - 4 * 1 * (-24)

D = 25 + 96

D = 121

x₁₂ =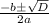

- первое число подходит, т.к положительное;

- число не подходит, т.к отрицательное.

Подставим первое число в условие X+5

⇒ x + 5 = 3 + 5 = 8 - второе число.

Произведение двух найденных чисел равно 24:

3 * 8 = 24

Одно число больше другого на 5:

8 - 5 = 3 - первое число;

3 + 5 = 8 - второе число;

ответ: Первое число 3, второе число 8.