Найти два двузначных числа, обладающих следующим свойством: если к большему искомому числу приписать справа нуль и за ним меньшее число, а к меньшему числу приписать справа большее число и затем нуль, то из полученных таким образом двух пятизначных чисел первое, будучи разделено на второе, дает в частном 2 и в остатке 590. Кроме того, известно, что сумма, составленная из удвоенного большего искомого числа и утроенного меньшего, равна 72. Если так записать условие, то получается иррациональный ответ:
Возможно, опечатка в "Кроме того, известно, что сумма, составленная из удвоенного большего искомого числа и утроенного меньшего, равна 72."
Возможно имелось ввиду что-то подобное:
""Кроме того, известно, что сумма, составленная из УТРОЕННОГО большего искомого числа и УДВОЕННОГО меньшего, равна 72"
Есть предложения...
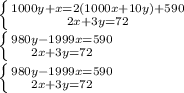
Ответы
Показать ответы (3)
Другие вопросы по теме Алгебра
Популярные вопросы
- Подготовьте сообщение на тему: Русский этикет в пословицах и поговорках...
3 - ответьте на 2 задание и на 3 задание у меня соч идёт до 12:00 нужно...
3 - Решить задачу: Велосипедист движется со скоростью 10 м/с. Какой...
3 - Задание No 1. Используя формулы разделите вещества на простые иСЛОЖНЫe:...
2 - 4. Решите уравнение: ЭТО СОЧ ДАМ ЛУЧШИЙ ОТВЕТ И ...
2 - Берілген стильдерді анықтамасыменсәйкестендіріңіз....
2 - Определите тему и идею предложенного отрывка из произведения. Как...
3 - с математикой x*(-6)+16,9=-8,9...
1 - 5 Решите уравнение: 12 + у139- 913=777713Решить уравнение в тетради5...
2 - Complete the sentences using the correct form (where necessary)...
2