найти четыре числа образующие геометрическую прогрессию у которой второй член меньше первого на 35 а третий больше четвертого на560
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. Как вы понимаете выражение: плотность гранита 2600 кг/м^3...
1 - Вычисли 99 162 x40 33-х 2027 h81 5 и - 4 1/2...
3 - Світосприйняття якого соціального зображено у прозі М. Булгакова?...
1 - Заполните пропуски словами в правильной форме.В 1 задание начинать с 9...
1 - 144В. Назовите профес- сиональные слова. Почемув стихотворении использу-ОТСЯвыделенные...
2 - Запиши пословицу,вставляя пррпушенное слово (антоним) Доброе слово лечит...
2 - Арифметические действия над рациональными числами. Урок 3...
3 - Используя рисунок, определите объём тела и вычислите его плотность. ответ...
3 - Объясните как это делать. Какие числа будут распечатаны? for i in range(2-2-1):...
2 - 2. Система отсчета связана с автомобилем. В каком из приведенных ниже случаев...
3
Два варианта:
7, -28, 112, -448
Объяснение:
q=±4,
b1=7, q=-4
b1=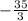 q=4
q=4
1) -35/3; -140/3; -560/3; -2240/3
2) 7; -28; 112; -448
Объяснение:
b₁, b₂, b₃, b₄-числа образующие геометрическую прогрессию⇒b₂=qb₁, b₃=q²b₁, b₄=q³b₁
b₁-b₂=35
b₃-b₄=560
b₁-qb₁=35
q²b₁-q³b₁=560
b₁(1-q)=35
q²b₁(1-q)=560
q²=560/35=16⇒q=±4
1) q=4
b₁=35/(1-q)=-35/3
b₂=qb₁=4·(-35/3)=-140/3
b₃=qb₂=4·(-140/3)=-560/3
b₄=qb₃=4·(-560/3)=-2240/3
2) q=-4
b₁=35/(1-q)=7
b₂=qb₁=-4·7=-28
b₃=qb₂=-4·(-28)=112
b₄=qb₃=-4·112=-448