Найти частное решение линейного дифференциального уравнения первого порядка:
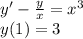
Другие вопросы по теме Алгебра
Популярные вопросы
- Какой из нижеприведенных углеводородов встречается в керосиновой фракции нефти?...
3 - Какие типы расположения почек ты знаешь?...
3 - 506-507 есеп шгарп бернш беремм...
2 - Вельми шановні Александр Глебовіч й Соф я Ігнатовна просимо Вас прийняти участь...
3 - В ящику лежать 5 пістолетів, з них 3 непристріляних. Ймовірність влучення у...
3 - Определите, какую форму устройства государства провозгласил Т. Джефферсон в...
2 - Task 3. Read the answers. Complete the questions in Past Simple Tense. 1. WhenMr....
1 - На сколько частей можно разрезать тыкву с ухмылкой одним разрезом? А двумя?...
1 - Лексичне значення слова поціновувач...
1 - Закодируй изображение юрты на листке в клетку с двоичного кода (графическое...
3
замена:
общее решение
частное решение