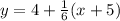Найти частное решение дифференциального уравнения: (x+5)dy=(y-4)dx x=1 y=5
Другие вопросы по теме Алгебра
Популярные вопросы
- Из ташкента в смарканд выехала нексия со скоростью 80 км в час одновременно...
3 - Напиіть твір (5-7 речень), який починався б словами люди різних професій...
1 - Командой-род число и часть речи...
3 - Расставьте пропущенные буквы и знаки препинания. подчеркните обособленные...
2 - ермек, который нес груз на машине, решил, что он сможет сдвинуть одну коробку,...
1 - Ть зробити синтаксичний розбі! 50 ів !...
2 - Построить график и подробно объяснить ход построения 100 заранее ток оч...
1 - Решить, эти 2 примера( нажмите на фото ) буду...
2 - Докозать 3)ctg l=cos l /sin l4)tg l × ctg l =1 6)1+ctg² l=1/sin² l...
3 - Нужно написать 4 предложения там где будет слово с приставкой при...
2
Дифференциальное уравнение является уравнение с разделяющимися переменными.
Разделим переменные: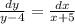
Проинтегрируем левую и правую части уравнения, получим:
Найдем теперь частное решение, подставляя начальные условия:
ЧАСТНОЕ РЕШЕНИЕ :