Найти частное решение дифференциального уравнения и вычислить значение полученной фукции у=ф(x) при Х=Хос точностью до двух цифр после запятой.
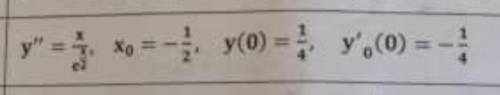
Другие вопросы по теме Алгебра
Популярные вопросы
- Отрезки ab и сd пересекаются в точке о, которая является серединой каждого...
3 - Найдите точку максимума функции y=(x+5)^2*(x-5)+9...
2 - Умиколи було 9 монет по 5 копи 8 монет по 10 коп,ск всього грошей було...
3 - Составить предложение со словами ветреный и ветряной ....
1 - Диагональ ac ромба abcd равна (под корнем 2+ корень из 3 ), а угол при...
2 - Акции предприятия распределены между государством и частными лицами...
3 - Сколько грамм цинка должно прореагировать с соляной кислотой, чтобы...
1 - Заменит фразеологизмы синонимичными словами и слосочетаниями: вставлять...
3 - Какое из чисел рациональное? ? 1)корень из 12 умножить на корень из...
3 - Что к отставке сперанского? назовите не менее 2х результатов первого...
2
По частям:
общее решение
частное решение
При
ответ: 0,35