Найдите значения а и b, при которых неравенство:
(x-a)(4x-1)(x+b)>0 имеет решение (-oo(бесконечность);-3) U (1/4(дробь);9)​

Нули выражения, записанного слева: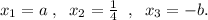  

Решение неравенства имеет вид: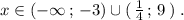  

Знаки  выражения, записанного слева, чередуются таким образом;

Поэтому в условии надо перед всей левой частью поставить знак минус, или записать  неравенство со знаком меньше, а не больше.

То есть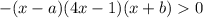     или     .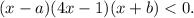

Тогда возможен вариант ответа:    .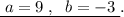

Вид неравенства: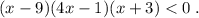  

P.S.  Либо неравенство можно было записать , например, так:

   или так    

Но заданное неравенство не будет иметь тот ответ, что записан в условии . Наверное, произошла описка и неравенство было задано со знаком меньше, а не больше.