Найдите значение выражения x^5y - xy^5/5 (3y - x) * 2(x - 3y)/ x^4 - y^4 при х = - 1/7 и y = -14 Я прикрепил изображение, чтобы было понятнее.
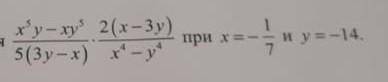
Другие вопросы по теме Алгебра
Популярные вопросы
- 6,8,9,10,11,12 менеджмент заранее надо сделать...
1 - Нужно сделать из чисел 692721 число ! максимум ...
3 - Wann kann ich viel geld bekommen und alles kaufen...
3 - Укажите предложения где правильно выделена грамматическая основа 8 класс...
1 - Розібрати слово автопарк за будовою...
3 - Сочинение-рассужение на тему: за какой поступок (в моем понимание) человеку...
2 - Точка находится на расстоянии 24 см от линзы фокусное расстояние которой...
2 - Два хоббита находились в лодке на берегу реки. к ним обратился отряд эльфов...
3 - Ясеньйор середньовіччя (твір)...
3 - 2. определение запаха и вкуса.возьмите небольшое количество меда и растворите...
2
x^5y - xy^5/5 (3y - x) * 2(x - 3y)/ x^4 - y^4
Подставляя значения, получаем:
(-1/7)^5*(-14) - (-1/7)*(-14)^5/5 (3*(-14) - (-1/7)) * 2((-1/7) - 3*(-14))/ (-1/7)^4 - (-14)^4
Далее, вычислим каждую часть по отдельности, начиная с числителей:
(-1/7)^5 * (-14) = (-1/7)^5 * (-14) = -0.00000226711 * (-14) = 0.000031734
(-1/7)*(-14)^5 = (-1/7)*(-537824) = 76832/7 = 10976
Теперь вычислим знаменатель:
3*(-14) - (-1/7) = -42 + 1/7 = -293/7
(-1/7)^4 - (-14)^4 = (-1/7)^4 - 38416 = 1/2401 - 38416 = -38399/2401
Теперь подставляем полученные значения в общее выражение:
(0.000031734 - 10976/5 * (-293/7) * 2 / (-38399/2401)
Сначала упрощаем числитель:
(-10976/5)*(-293/7)*2 = (10976*293*2)/35 = 11091424/35 = 316040
Теперь заменяем все значения в общем выражении:
0.000031734 + 316040 / (-38399/2401)
Делаем общий знаменатель для сложения дробей:
0.000031734*(-38399/2401) + 316040 / (-38399/2401)
Выполняем сложение дробей в числителе:
(-0.00818705136666 + 316040) / (-38399/2401)
Упрощаем числитель и заменяем числовое значение итоговой дроби:
315031.99181294877 / (-16.074749282038905)
Наконец, выполняем деление:
315031.99181294877 / (-16.074749282038905) = -19570.298923698155
Ответ: значение данного выражения при x = -1/7 и y = -14 равно -19570.298923698155