1. Алгебра
  2. Найдите значение выражения

Найдите значение выражения (x-1)(x^2+1)(x^4+1)(x^8+)/15 при х=14

Chundokova Chundokova    2   10.03.2019 10:10    6

Ответы
Hacтяя Hacтяя  24.05.2020 16:17

Раскроем скобки в уменьшаемом:

 

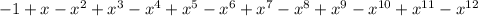
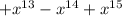
(x-1)(x^2+1)(x^4+1)(x^8+1) = -1+x-x^{2}+x^{3}-x^{4}+x^{5}-x^{6}+x^{7}-x^{8}+x^{9}-x^{10}+x^{11}-x^{12}+x^{13}-x^{14}+x^{15}

 

Уменьшаемое - это геометрическая прогрессия. а1=-1, а15=-х^{15}, d=-х

Сумма данной прогрессии равна:

 

S=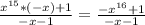 \frac{x^{15}*(-x)+1}{-x-1} = \frac{-x^{16}+1}{-x-1}

 

\frac{-x^{16}+1}{-x-1} - \frac{x^{16}}{15} = \frac{15(1-x^{16})+x^{16}*x+x^{16}}{-15(x+1)} = \frac{15-15x^{16}+x^{17}+x^{16}}{-15(x+1)} =\frac{15-14x^{16}+x^{17}}{-15(x+1)}

 

Подставляем х=14 и получаем:

 

\frac{15-14*14^{16}+14^{17}}{-15(14+1)} = \frac{15-14^{17}+14^{17}}{-15*15} = \frac{15}{-15*15} = -\frac{1}{15}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Medvedevalilit2004 Medvedevalilit2004  13.03.2019 14:10
Веселопедист проехал семь пятнадцатых пути и ещё 40 км , и ему осталось проехать 0,75 пути без 118км. как велик этот путь? , нужно...
YanaDovgik YanaDovgik  13.03.2019 14:10
Обчислите значение производной функции в точке х0,если f(х)= √3 * sinx+x^2/п+xsinп/6 x0=п/3...
v2an87 v2an87  13.03.2019 14:10
Сократите дробь: (25y^2-4)/(25y+10)...
Рената1701 Рената1701  13.03.2019 14:10
Решите уравнение cos(3x+π)-cos5x+√2sin(4x+3π/2)=0 укажите его корни,лежащие в промежутке [π/2; π]...
smalik8 smalik8  13.03.2019 14:10
При каком значении переменной дробь равна 0 x+1/x(в квадрате)+1 если есть возможность, объяснить последовательность действий заранее ! : )...
Снежана21111 Снежана21111  13.03.2019 14:10
Cos(в квадрате) 150(градусов)- sin(в квадрате) 150(градусов)...
STASік STASік  13.03.2019 14:10
Моторная лодка по течению реки 10 км, а против течения 15 км, затратив на весь путь 3 ч 20 мин. найдите собственную скорость моторной лодки, если скорость течения равна 3 км/ч. сделать,...
fdimon fdimon  13.03.2019 14:20
Величина х-467 уменьшена на 70%.чему теперь примерно равно значение х...
apakovaleria apakovaleria  17.04.2019 22:41
Объемы каких понятий находятся в отношении подмножество​...
таня1966 таня1966  17.04.2019 22:39
27x^4-3x^2 =0 решите неравенство...

Популярные вопросы