Найдите значение выражения
tg(1/2arcsin(24/25) + 3arctg(1/2))
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите х. Решите задачу по геометрии 8 класс...
2 - Общие свойства воды и полиэтилена...
3 - 1. Where do you live ? (where/you/live) 2. . . . . . . . . . . . . ....
3 - У прямокутному трикутнику AC з гіпотенузою проведино бісектрису CK гіпотеза...
3 - 8.Найдите значения выражения...
2 - 3)|-3,5|*|-7/8|*1,6 и |-8,1+32|*0,01; 4)|49,2-50|:|-0,4| и 201 - 401|*0,1...
2 - Укр. мова заболотний 2021 впр 396...
2 - Посмотри любой рекламный ролик в Интернете, по телевизору Определи цель...
1 - Выбрать 1 календарно-обрядовую песню, выписать её(если большая,то отрывок),...
3 - 51 Найди ложные общие утверждения и приведи для них контрпример. Сформу-...
2
Нам могут понадобиться такие формулы:
Первая из них выводится из формул синус суммы и косинус суммы, вторая является частным случаем первой, третья выводится из первой и второй. Каждая из них справедлива при тех значениях переменных, при которых существуют обе части равенства. Конечно, неплохо бы знать формулу тангенс половинного аргумента. Она выводится из второй выписанной формулы, но мы постараемся обойтись без нее.
Чтобы дальше не мучиться, найдем отдельно tg(3arctg(1/2)):
Заметим, что arcsin(24/25) - это угол прямоугольного треугольника с гипотенузой 25 и противолежащим катетом 24. По теореме Пифагора находим второй катет b²=25²-24²=(25-24)(25+24)=49; b=7 (многие, конечно, прямоугольный треугольник 7-24-25 помнят наизусть так же хорошо, как и египетский 3-4-5). Нас интересует половина этого угла, то есть угол между катетом b=7 и биссектрисой. Как известно, биссектриса делит сторону a=24 на отрезки x и 24-x, пропорциональные боковым сторонам: x:(24-x)=7:25; x:24=7:(7+25);
x=21/4. Поэтому tg((1/2)arcsin(24/25))=(21/4)/7=3/4, то есть половина арксинуса 24/25 равна арктангенсу 3/4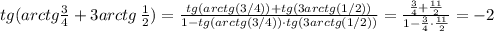 .
.
ответ: - 2