Найдите значение выражения: tan1°tan2°...tan89°
Другие вопросы по теме Алгебра
Популярные вопросы
- Запишите все правильные дроби со знаменителем 7...
3 - Какое значение имеет биология? (ответ для 5 класса, .)...
2 - Тоскает, зверёк, листва, сухая, туда. из, мох, постель, мягкая,...
1 - Что важнее в семье кнут или пряник? эссе...
3 - 25 і! 1)деякі мухи схожі на бджіл і дзижчать як бджоли; 2)тварини...
1 - Вычисли площадь и периметр фигур. ширина 3см длина 4см длина 2см...
1 - Можно ли жить в обществе без права? почему?...
1 - Придумать предложение с словами (барва осенні)...
3 - Какие ткани состоят из этих клеток?...
3 - Как взаимосвязаны между собой такие абиотические факторы какитемператураи...
2
Поменяем местами множители:
Преобразуем некоторые тангенсы:
Воспользуемся формулой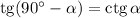 :
:
Воспользуемся формулой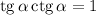 , а также табличным значением
, а также табличным значением 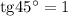 :
: