Найдите значение выражения корень из 48 - корень из 192 sin^2 pi/12
Другие вопросы по теме Алгебра
Популярные вопросы
- Может ли диагональ трапеции разделить пополам её среднюю линию?...
2 - 8-го класса .какое количество воды в моль получится при взаимодействии...
3 - Какой закон нарушил пётр и понёс наказание в повести о петре и...
2 - Сочинение на тему что такое для меня родной город...
3 - Какой признак не характерен для животных, населяющих переувлажненные...
2 - Как правильно сделать? тема-сокращение дробей. : сократите дробь...
1 - Одним из итогов кавказской войны было войны было: 1. поражение...
3 - Определите массу mg3n2, полностью подвергшегося разложению водой,...
3 - Describe any two members of your family use: i think , usually...
2 - Как правильно писать кузнечики стрекочат или стрекочут...
3
Использую косинус двойного угла
√48-√192 sin²π/12 = √48(1-2sin²π/12) = 4√3(cos(π/6)) = 4√3*√3/2=2*3 =6
Ещё один вариант решения.
Так как по формуле понижения степени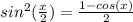 , то
, то 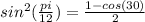 , откуда получаем:
, откуда получаем:
Теперь подставим данное значение в выражение, вместо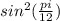 .
.
ответ: 6.