Найдите значение выражения: 4sin, если cos=1/4 и ∈(3П/2;2П)

Question

Алгебра: Найдите значение выражения: 4sin, если cos=1/4 и ∈(3П/2;2П)

Azozylya · Answer

Есть основное тригонометрическое тождество sin² x + cos ² x = 1

Выразим отсюда sin х

$sinx = \sqrt{1-cos^{2}x }$

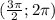Т.к. x∈ $(\frac{3\pi }{2} ; 2\pi )$ ⇒ sin x будет положительным (а косинус должен быть отрицательным по идее, но на синус знак косинуса не особо влияет)

$sinx = \sqrt{1-(-\frac{1}{4} )^{2} } = \sqrt{\frac{16-1}{16} } = \sqrt{\frac{15}{16} } = \frac{\sqrt{15} }{4}$

Получается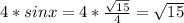 $4*sin x = 4*\frac{\sqrt{15} }{4} = \sqrt{15}$

ответ: √15

Найдите значение выражения: 4sin, если cos=1/4 и ∈(3П/2;2П)

Популярные вопросы