1. Алгебра
  2. Найдите значение выражения

Найдите значение выражения -4√3sin(-780)

kburuncenco307 kburuncenco307    3   05.10.2019 08:20    9

Ответы
niganai niganai  09.10.2020 21:19

ответ: 6

Подробное решение:

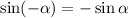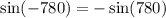1) Воспользуемся формулой приведения \sin(-\alpha)=-\sin\alpha. Получим: \sin(-780\degree)=-\sin(780\degree).

2) Воспользуемся ещё одной формулой приведения: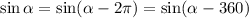 \sin\alpha=\sin(\alpha-2\pi)=\sin(\alpha-360\degree). Получим: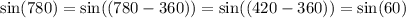 \sin(780\degree)=\sin((780-360)\degree)=\sin((420-360)\degree)=\sin(60\degree)

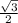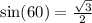3) Так как синус угла 60° - табличное значение, равное \frac{\sqrt{3}}{2}, то справедливо выражение: \sin(60\degree)=\frac{\sqrt{3}}{2}.

4) Подставляем вычисленный синус в выражение:

-4\sqrt{3}(-\frac{\sqrt{3}}{2})=\frac{4*3}{2}=2*3=6

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
1NatikNatik1 1NatikNatik1  03.09.2020 15:19
Проведіть прямі а іь так, щоб вони перетиналися. По- значте точку їхнього перетину буквою C. Чи належитьточка С прямій а? прямій b?​...
brigr brigr  03.09.2020 15:19
По действиям................ ​...
KotekaClient KotekaClient  03.09.2020 15:19
Даны векторы a→(−8;−5;2), b→(3;−4;1), c→(8;−8;−3) и d→(3;4;−4). Вычисли координаты данных векторов: a→+c→{ ; ; }; a→+b→+d→{ ; ; }; a→+b→+c→+d→{ ; ; }....
макс3104 макс3104  03.09.2020 15:15
Y-x=20,2x-15y=110x-9y=821y+15x=0,5​...
mrmersbrady mrmersbrady  03.09.2020 15:15
Квадратные уравнения 1.задание 9 №137383 решите уравнение x2-x-6=0 Если корней несколько,запишите их в ответ без пробелов в порядке возрастания...
хорошист548 хорошист548  03.09.2020 15:15
Y=2,5 до ть розвязати на тему:графіки лінійних функцій​і y=-1 1/4...
сюрприз23456789 сюрприз23456789  03.09.2020 15:15
Упростите выражение (4а*2-3)+(5-а-2а*2)​...
совуша2007 совуша2007  04.09.2020 15:22
9. Теңдеуді шешіңдер:а) 2x2 = 5x; б) 0,49 - х = 0;ә) 0,3х2 = 7,5х;в) – 25 = 0.​...
artyomka12 artyomka12  03.09.2020 15:15
Линейная функция и её график у=2х+1​...
Батюс Батюс  03.09.2020 15:15
Ние этих Упражнения для повторения 1.37. Функция задана формулой f (x) = -3х2 + 2х. адратов 1) Найдите: f(1): f(0): ()f(-2). f ищут 2) Найдите значения аргумента, при которых значение...

Популярные вопросы