Найдите значение выражения: 2㏒²7 (49)=?
Другие вопросы по теме Алгебра
Популярные вопросы
- I. decide whether the statements are true ( + ) or false ( – ). 1. the greatest...
1 - Как пользоваться календарем из мамонтовой кости...
3 - ответить на тесты: 21. выберите вариант. die veränderungen haben begründete erläuterungen....
1 - Речення про птахів в переносному значіні...
2 - Весной было 17 дождливых дней.в мае три а в марте и апреле поровну.сколько дождливых...
2 - Написать краткое(небольшое) сообщение о любой народности сибири...
1 - Удельная теплоемкость платины равна 140 кг / дж × градус цельсия это означает,что...
2 - 3а в квадрате • 2b в квадрате • 0,25 аb?...
1 - Запишите числа и представьте их в виде суммы разрядных слагаемых 27050 и 50004...
2 - Нужно 1) можно ли прожить без конфликта в школе? (и как то объяснить это) 2) нужно...
1
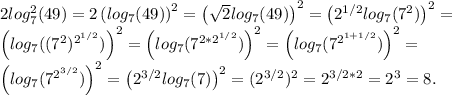
ответ: 8.Пример из комментариев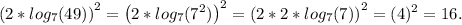
ответ: 16.Второй пример из комментариев.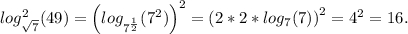
ответ: 16.