Найдите значение выражений,если tg=2:

Другие вопросы по теме Алгебра
Популярные вопросы
- Рассчитайте,какую массу будет иметь при н.у. 5,6 л кислорода...
3 - Почему продолжительность рабочего времени установлена правительством рф?...
3 - Вставте слово,которое служило бы окончанием первого и одновременно началом...
2 - Какое количество информации несет сообщение встречаемся 17 октября ?...
1 - Виктор петрович едет в автобусе уже 30 мин. во сколько он приедет на свою...
2 - Примеры героизма из современной общественной жизни....
2 - 7) шестой член арифметической прогрессии составляет 60% от третьего, а...
2 - Редактирование текста представляет собой...
3 - Найдите координаты точек пересечения с осями координат графика функции...
1 - Фонетичесский разбор слова юла, , !...
3
Разделим дробь на cos α, мы получим
Далее воспользуемся известным тождеством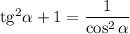
ответ: 21/40.