1. Алгебра
  2. Найдите значение углового

Найдите значение углового коэффициента касательной к графику функции у=f(x) в точке с абсциссой x0

, x0=2


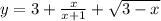
y = 3 + \frac{x}{x + 1} + \sqrt{3 - x}

dzeratigieva dzeratigieva    2   02.09.2021 15:47    4

Ответы
dogmisha228 dogmisha228  06.10.2021 01:40

k=-\frac{7}{18}

Объяснение:

Значение углового коэффициента равно значению производной в точке х₀.

Используем формулы:

\displaystyle (C)'=0,\;\;\;C-const\\\\(\frac{u}{v})' =\frac{u'v-uv'}{v^2}\\\\(u^n)'=nu^{n-1}*u'

\displaystyle y=3+\frac{x}{x+1}+\sqrt{3-x}=3+\frac{x}{x+1}+(3-x)^{\frac{1}{2} }\\\\

Найдем производную:

\displaystyle y'=0+\frac{x'*(x+1)-x(x+1)'}{(x+1)^2} +\frac{1}{2}(3-x)^{-\frac{1}{2} } *(3-x)'=\frac{1(x+1)-x*1}{(x+1)^2} +\frac{1}{2\sqrt{3-x} } *(-1)=\frac{1}{(x+1)^2}-\frac{1}{2\sqrt{3-x} } }

Найдем значение функции в точке х₀:

\displaystyle y'(x_0)=y'(2)=\frac{1}{(2+1)^2}-\frac{1}{2\sqrt{3-2} } =\frac{1}{9}-\frac{1}{2}=\frac{2}{18}-\frac{9}{18}=-\frac{7}{18}

\displaystyle k=y'(x_0)=-\frac{7}{18}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
БеднаяЕва БеднаяЕва  11.09.2019 00:10
При якому значенні а рівняння (х+2)(х--2)(х+4)=ах має безліч коренів?...
DimanGuy32 DimanGuy32  11.09.2019 00:10
121+100-2*11*10*157черта дроби 220=? напишите какой будет ответ и как получили это число...
sempai1 sempai1  11.09.2019 00:10
Какие из точек принадлежат графику функции, заданной формулой у=4х+2. а)(1: 6) : 6) в)с (-1: 6) г)(d 1: 2)...
HanNazbi HanNazbi  26.09.2019 01:40
Разложить на множители 36m²n³ - 49m⁴n...
Okean111 Okean111  26.09.2019 01:40
Обчисліть значення виразу 1/3х + 1/4у якщо х=24 у=-16...
минам2003 минам2003  26.09.2019 01:40
Преобразуйте в многочлен выражение (5с - 2)^2 ^-степень...
svetlanavikuli svetlanavikuli  28.09.2019 05:20
Найти координаты точки пересечения графиков функций y＝1.5x-3.9 y＝5.4-1.6x...
ddurua ddurua  28.09.2019 05:20
Одно число при деление на 10 дает остаток три другое число при делении на пять дает остаток два докажите что сумма этих чисел делится на пять...
angelikamaxowoz4v angelikamaxowoz4v  28.09.2019 05:20
Решить уравнения по 1) |x|+3=2 2) 4|x|-7=0 3) 3|x|+2=0 4) |3x+5|-2=0 5) |2x-5|+3=8...
UtkinaVioletta UtkinaVioletta  28.09.2019 05:20
Найдите углы параллелограмма abcd, если: угол а = 2уголв...

Популярные вопросы