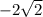Найдите значение производной функции f(x)=6cos x +2sin x при х= пи/4
fire31
3
06.10.2019 04:40
1
Другие вопросы по теме Алгебра
ImHomme
20.08.2019 15:50
Аниса2111
20.08.2019 15:50
dragons55u
20.08.2019 15:50
34224253
20.08.2019 15:50
Katуа07
20.08.2019 15:50
евгения2066
15.05.2020 17:19
Кек11111111118
15.05.2020 17:18
Популярные вопросы
- Ребят умоляю, у меня контроша...
2 - 2. Підвищує частоту і силусерцевих скорочень:А) інсулін,б) тестостерон;в)...
2 - На рисунке изображены график функции y=f(x) и касательная к этому графику,...
1 - На дно бассейна, длина которого 17 метров, это на 8 метров больше, чем...
3 - Найди и объясни знакомые орфограммы. Мы тогда лишь дышим, Когда речь...
3 - ВЕ и СF высоты АВС. При только линейки постройте высоту АХ этого треугольника....
1 - Почему рассказ Солдатёнок имеет такое название...
1 - Даны точки: C(5;−36) , K(−36;5) , M(5;18) , L(−36;−34) . Определи, которая...
3 - Напишите отзыв о прочитанном произведении.Козлов В.Ф. «Сократ мой друг»....
1 - Кометаны сипаттап жазу керек. Көмектесіңіздерші...
3
f(x) = 6cosx + 2sinx, x₀ = π/4
f'(x) = -6sinx + 2cosx
f'(x₀) = f'(π/4) = -6sin(π/4) + 2cos(π/4) = -6 · √2/2 + 2 · √2/2 = -3√2 + √2 = -2√2
ответ-2√2
Найдём производную f'(x)
Подставим в f'(x) x = π/4
ответ: