1. Алгебра
  2. Найдите значение параметра

Найдите значение параметра а(а>0), при котором площадь фигуры ограниченной графиком функции у=а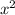x^{2}+2 и прямыми х=-2; х=-1; у=0, равно 31/12

ксения1291 ксения1291    2   13.01.2022 21:12    0

Ответы
Вывыия Вывыия  13.01.2022 22:00

S=\int\limits^{-1}_{-2} {(ax^2+2)} \, dx =(a\frac{x^3}{3}+2x)| ^{-1}_{-2}=a(\frac{(-1)^3}{3}-\frac{(-2)^2}{3})+2(-1-(-2))=\frac{7}{3}a+2

По условию

S=\frac{31}{12}

\frac{7}{3}a+2=\frac{31}{12}

\frac{7}{3}a=\frac{31}{12}-2frac{7}{3}a=\frac{31-24}{12}frac{7}{3}a=\frac{7}{12}a=\frac{1}{4}


Найдите значение параметра а(а>0), при котором площадь фигуры ограниченной графиком функции у=а+2
ПОКАЗАТЬ ОТВЕТЫ
Dаniеll Dаniеll  13.01.2022 22:00

вам задана криволинейная трапеция. найдя ее площадь и приравняв  к 31/12 , можно ответить на ваш вопрос. итак, площадь считаем через определенный интеграл от -2 до -1 от функции (ах²+2-0) , он равен ах³/3+2х, по формуле Ньютона - Лейбница находим определенный интеграл.

S=((-1)³*а/3+2*(-1))-((-2)³*а/3+2*(-2))=-а/3-2+8а/3+4=2 +7а/3

2 +7а/3=31/12

24+28а=31

28а=7, значит. а =0.25

ответ при а=0.25

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
pourkur1111oz10kt pourkur1111oz10kt  28.09.2019 16:50
Масса меди, цинка и никеля в сплаве пропорциональна числам 13; 4; 3. рассчитайте массу сплава, если вы знаете, что медь на 500 г больше никеля!...
seanius seanius  01.08.2019 23:10
20 , молю найдите координаты точек пересечения с осями координат 1)y=-15x-6 2)y=70x+35...
anuta00002000 anuta00002000  01.08.2019 23:10
Решить квадратное уравнение x(x-5)=1-4x...
vershinindaniil1 vershinindaniil1  19.05.2020 17:54
Выбери пару натуральных чисел, которая удовлетворяет уравнению x+y=15. ответ: (3;5) (17;−3) (0;16) (4;11) (−6;22) (−9;−6...
Арти1234567890 Арти1234567890  19.05.2020 17:54
Дополни словесную модель по математической: {4x+6y=46 3x−2=2y Две бригады работали на уборке капусты. В первый день одна бригада работала 4 ч., вторая — 6 ч., и собрали...
мошкада мошкада  19.05.2020 17:53
Розвязати систему підстановки! Варіанти: (1;2) (2;1) (-2;1) (2;-1)...
kosmoz2005 kosmoz2005  19.05.2020 17:53
сложение решите систему линейных уравнении:...
karinai98 karinai98  19.05.2020 17:53
Нужно решить три последних примера.е) x-y/2b * 6a/x-yж) (x-y/2a)^2 : x-y/8a^2з) 4a^2/2a-b * 4a^2-b^2/12a^3 : 2a^2/6a^2-3ab...
vovabondar28 vovabondar28  29.04.2020 13:54
Вектор а равно 5, вектор б равно 12 найти сумму векторов, а перпендикулярно б...
dianadidi3 dianadidi3  29.04.2020 13:54
Для каждого неравенства укажите множество его решений a)x^2+4 0 b)x^2-4 0 c)x^2-4 0 f)x^2+4 0...

Популярные вопросы