Найдите значение х ,при котором f(x)=0 ,если f(x)=2^х+1*3^4х-9*6^2х
Ответы
f(x)=2^(х+1)*3^(4х)-9*6^(2х)
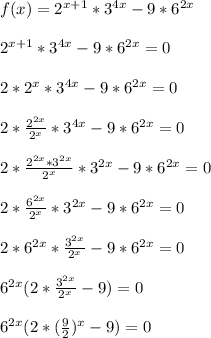
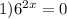 решений не имеет
решений не имеет
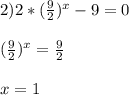
ПОКАЗАТЬ ОТВЕТЫ
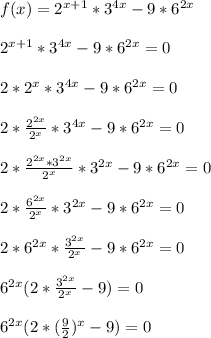
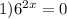 решений не имеет
решений не имеет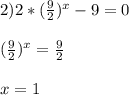
Другие вопросы по теме Алгебра
Популярные вопросы
- Дайте оценку влияния климата на жизнь и хозяйственную деятельность человека....
1 - Если смешать 10 см3 воды и 20 см3 спирта, какой будет плотность смеси? (d...
2 - Соч по математике 6 класс 2 четверть...
3 - Как определиться с выбором профессия Эссе 120 слов...
1 - «Подумайте!». Выберите грамматически правильные продолжения предложений....
2 - У чому особливість зберігання врожаю різних видів культур? 7речень...
3 - Бир ончой бышыктооч деп эмне айтабыз? коротко...
1 - Упростите выражение -6,2(х-1,5) + 4,5(1,6х – 0,4) -8,5 и найдите его значение...
3 - СОЧ) No4 Решите задачу составив уравнение: Периметрчетырехугольника АВСД...
2 - Определите, какой объем углекислого газа содержится в 5 моль этого газа?...
2